
情報処理安全確保支援士試験(SC)
令和5年 春期 AM1 問7
NAND素子を用いた次の組合せ回路の出力Zを表す式はどれか。
$$ここで,論理式中の「・」は論理積,「+」は論理和,「\overline{ X }」はXの否定を表す。$$
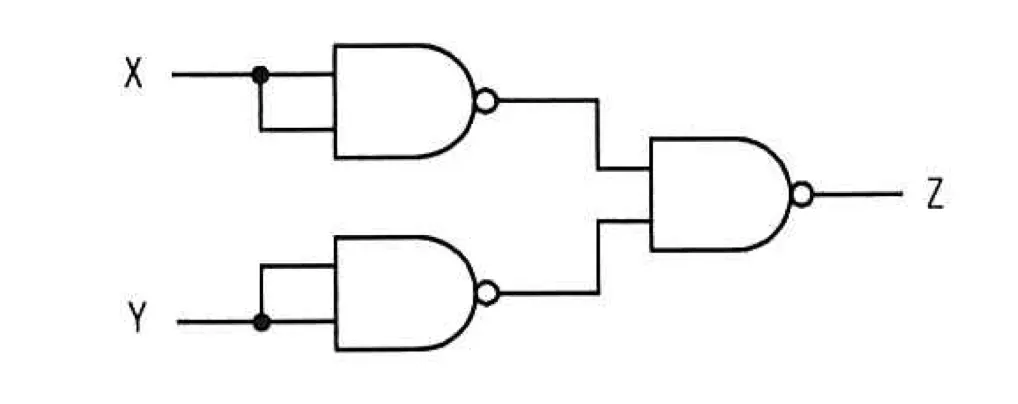
$$ア X・Y イ X+Y ウ \overline{X・Y} エ \overline{X+Y}$$
解答:
イポイント:
NANDゲートは、ANDゲートとNOTゲート(反転ゲート)の組み合わせから構成され、多くの論理回路やコンピュータシステムで基本的な論理ゲートとして使用されます。NANDゲートは、2つの入力を受け取り、次のように真理値表で表現されます。
| 入力A | 入力B | 出力 |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
この表に示されているように、NANDゲートは次のようなルールに従います:
- 入力Aと入力Bがどちらも0の場合、出力は1になります。
- 入力Aと入力Bのいずれかが1の場合、出力は1になります。
- 入力Aと入力Bがどちらも1の場合、出力は0になります。
NANDゲートは、ANDゲートとNOTゲート(反転ゲート)の組み合わせから構成され、多くの論理回路やコンピュータシステムで基本的な論理ゲートとして使用されます。
NANDゲートとは、論理積のNOTです。(掛け算してNOT)
全ての組み合わせを NANDゲートに入力すると、次の表が得られます。
| 入力A | 入力B | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
この表は、論理和の真偽表と同一です。そのため正解は、イ X+Y です。
関連資料:
更新日:2023-09-06